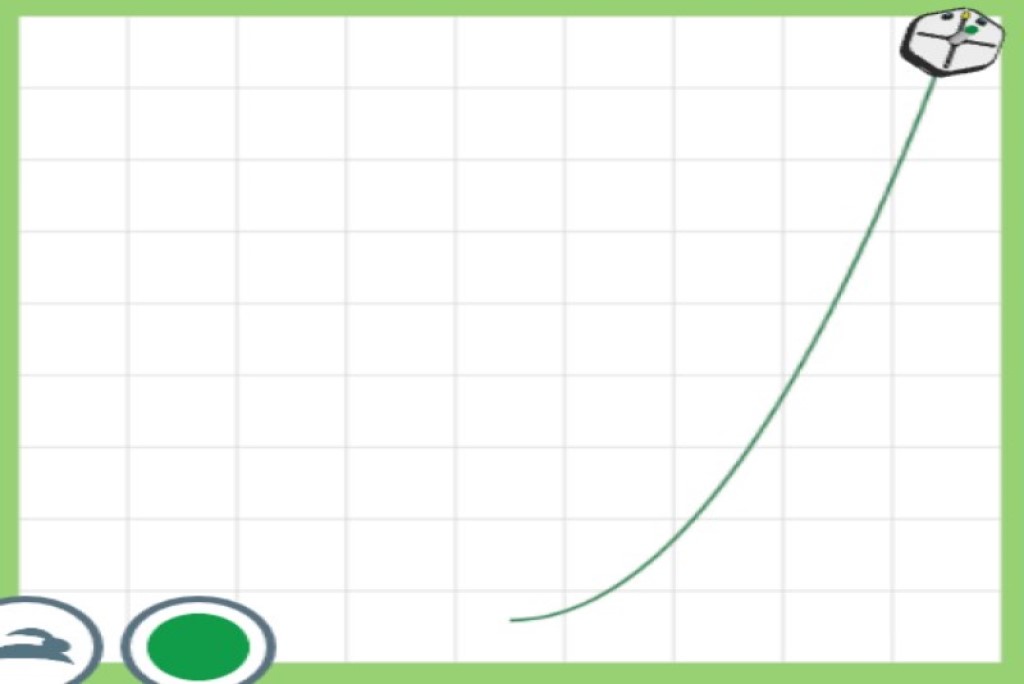
直線、曲線、繰り返し、などのプログラミングの基礎、センサーの基礎しか勉強できないと思っていませんか?
そんなことありません。
実はRootでは関数の勉強もできるんです!!!
数学の勉強なんかしたくないよ
そんなこと言わずに、Rootと数学を組み合わせたプログラムをぜひ見ていってください!
Rootの隠れた機能
隠れた機能とはいっても、普通に説明書に載ってます。
自身の位置を原点(0,0)と認識する機能です!
確かにその通りです。
僕も取扱説明書を見た時は「何言ってんの?」ってなりましたからね。
ですが、色々と考えていくうちに、数学の勉強ができるのではないか?と思いついたわけです。
数学の勉強に使えるブロック
「ナビをセットx○○,y△△センチ」


実はこのブロックは、Rootが移動する向き、距離を座標で指定できるという機能なんです!
例えば、(3,4)と指定すると、この位置まで直線でRootが移動します。
自分の位置が(0,0)なので、3cm左、4cm上の位置に一直線に向かいます。
ですが、このままでは一次関数になってしまいます。
二次関数を作るには
この機能を使って二次関数を作るには、ちょっと難しいプログラムを使わないといけません。
「変数」です。


この変数の使い方を理解するのにかなり時間がかかります。
僕もいまだに正確には理解できてないですからね。
とりあえず二次関数を書くくらいの使い方ならわかったので書いていきたいと思います。
まずは答えのプログラムを載せます。
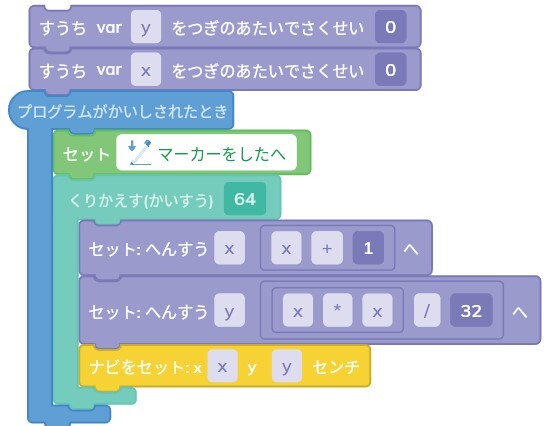

多分答えを見てもすぐに理解できるレベルじゃないと思います。
すぐに理解できる人はこんな記事読まずに自分でもっと難しいプログラムを考えてください。
ではそれぞれ解説していきます。
へんすうの使い方
まずは「セット:へんすうmy_number 0へ」の使い方です。


これをプログラムを組む画面にもっていくと、必ず一番上に「すうちvar my_numberをつぎのあたいでさくせい0」というブロックも作成されるはずです。
これは、変数の初期値を決めるブロックです。
基本的に何もいじらなくても大丈夫です。
今回の場合は二次関数を書くので2つの変数xとyを作りましょう!
名前の変え方は、「my_number」の部分をクリック→なまえをへんこうしますをクリック。
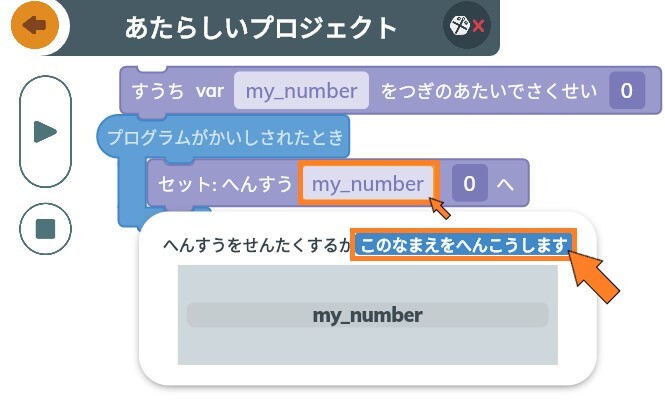

xを入力してEnterで完了です。
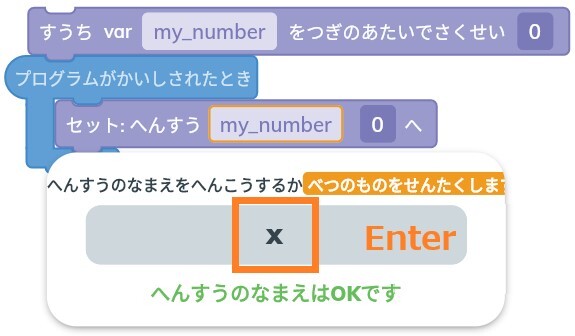

これで2つの変数ができました。
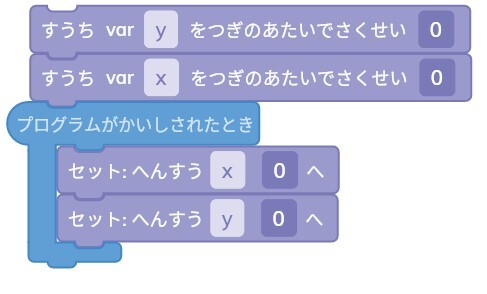

それについては今から説明していきます。
xとyの関係性をプログラム
次にxとyの関係をプログラムしていきます。
二次関数なので、y=ax^2+bという関係です。
今回は基本的な二次関数「y=ax^2」にします。
このくらいの式ならほとんどの人が理解できると思いますが、これをどうやってRootのプログラムで表現するかが難所です。
操作方法がよくわからないですからね…
xをプログラム
まずはへんすうx(エックス)をプログラムします。
xは初期値0で作成されています。
プログラムを開始した時にxが1になるようにします。
「セット:へんすうx0へ」に入力した値にxが変化します。
ここに1を入れれば、xに1を代入できます。
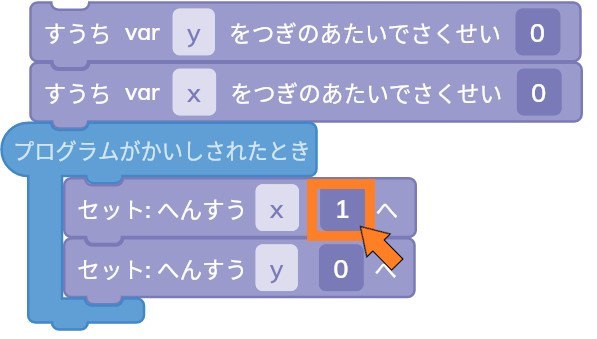

ただ、これだと永久にxが1のままになってしまいます。
グラフを書くにはxの値を変化させないといけません。
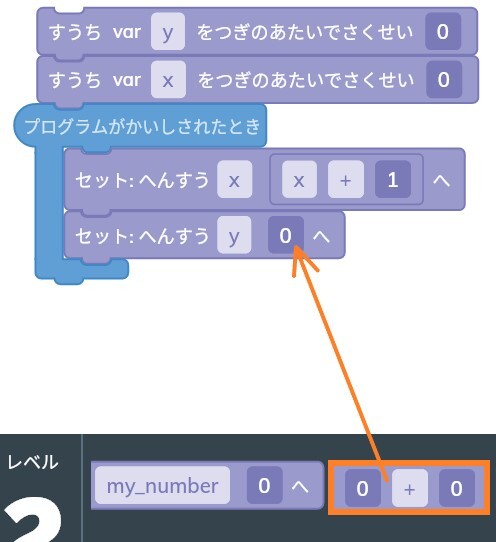
そういう場合は「0+0」のブロックを使ってプログラムを作ります。


この「0+0」ブロックをへんすうxの0の部分に持っていきます。


そして、この「0+0」にへんすう「my_number」をドラッグして入力します。
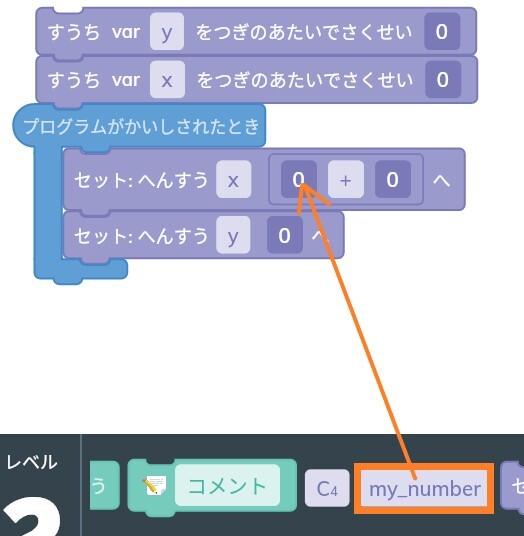

そのあとに「my_number」をクリックしてxに変更しましょう。
右側の0は1に変えます。
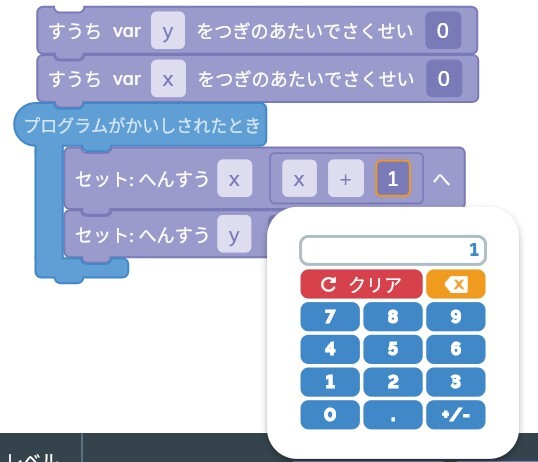

これで、式はx+1になりましたね!
この式は、「x=x+1」という意味です。
そうなんです。
数学の式としては成り立ってないんですが、プログラミング言語ではよく使われる形です。
プログラミングの世界では「xに代入する」という意味です。
今回の式「x=x+1」は「今のxの値に+1して下さい」という意味になります。
要するに、xが1ずつ変わっていくプログラムを作成したというわけです。
最初からそう言えよ



へんすうyをプログラム
yはx^2です。
つまり、xかけるx。
このyを作っていきましょう。
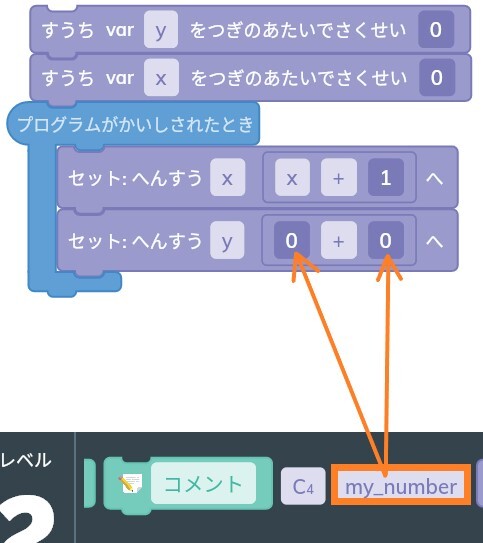
xの時と同じように、「0+0」を入力。

今回の場合は両方の0にxを入力します。

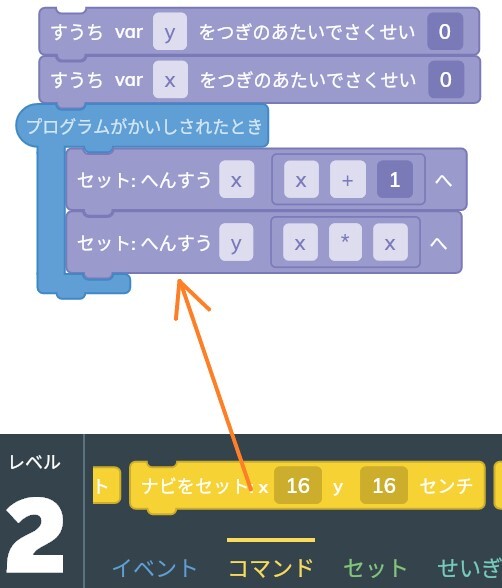
そして、+を*(×(かける)という意味)に変えます。
これで、y=x*x二次関数が完成しました!
おさらい
今作った所までのプログラムをおさらいしましょう。
今までのプログラムがあらわしているのはこういう内容です。
へんすうx、yを0でさくせいしなさい
へんすうxはプログラムを開始したら+1しなさい
へんすうyはxかけるxのあたいにしなさい
二次関数っぽくなってきましたね!



Rootを座標(x,y)に移動させる
そして、へんすうで作った場所にRootを移動させます。
「ナビをセット:x16y16センチ」のブロックを使います。

この数値の部分をxをへんすうx、yをへんすうyに設定します。
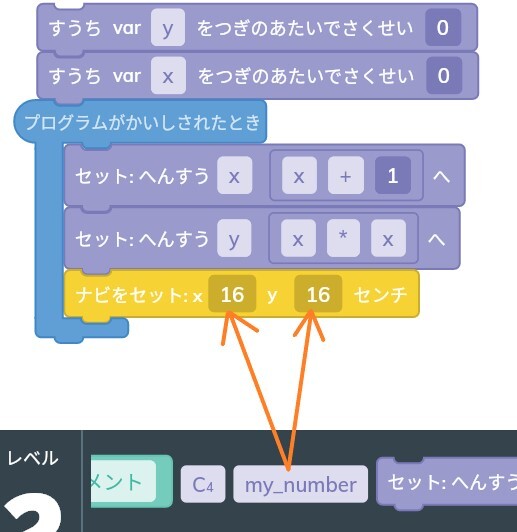

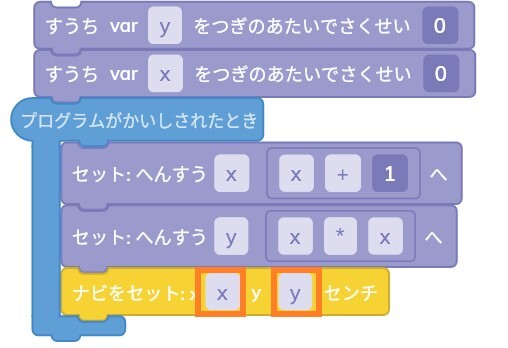

こうすることで、「今作ったへんすうの座標(x,y)に移動する」というプログラムが完成します。
さっそく実行してみましょう!



まだまだ完成には程遠いですよ!
繰り返す
今までのプログラムでは「プログラムがかいしされたとき」しか値が変化しません。
x=1、y=1で終わってしまいます。
これでは1次関数です。
なので、へんすうxの値を何度も変化するようにします。
そんな時に使うのが「くりかえす(かいすう)」ブロックです。
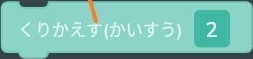

くりかえすでへんすうを囲むことで、x=x+1を何度も計算するようにできます。
とりあえず繰り返す回数を10に設定しておきましょう。


最後に、グラフを書くために、「マーカーをしたへ」ブロックを入れます。
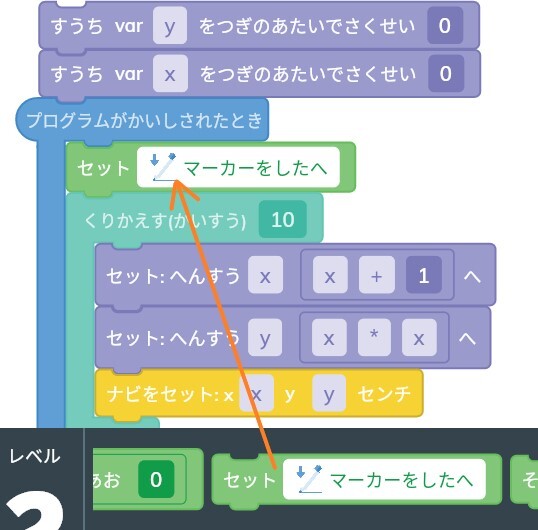

これでRootに二次関数を書かせるプログラムの完成です!
さっそくデモ画面で書かせてみましょう!
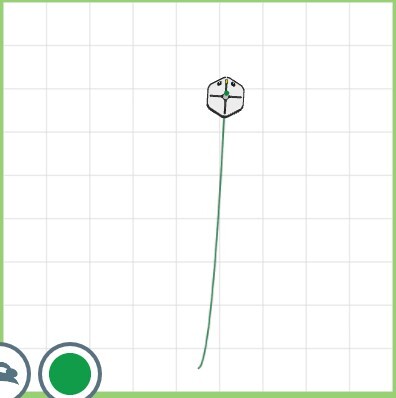

こうなりましたよね?
そうなんです。このままだと、もの凄く細長い二次関数が書かれてしまします。
そんなあなたにもっときれいにする方法を教えましょう。
なんであんなに細長くなるの?
Rootは座標で移動する「ナビをセットx○○,y△△センチ」はセンチ単位で動きます。
Rootのデモ画面にあるマス目は1マス16㎝です。
ということはどういうことかわかりますか?
x座標が1マス分(16㎝)変わると、y座標は16×16=256㎝も変化します。
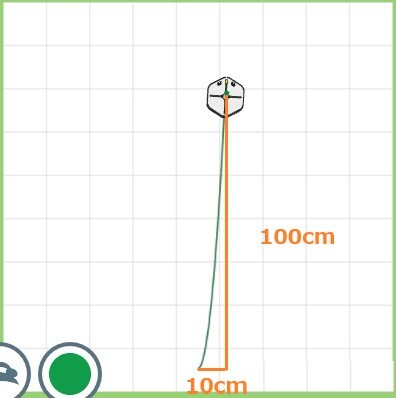

これではすぐに上に飛び出していきます。
二次関数の増加のすごさが分かりますね!
こういったことも実際に体験すると
という感覚を身に着けることができます。
貴重な体験です。
Rootでちょうどいい二次関数のグラフを書く方法
イイ感じの二次関数のグラフを書くには単純にyの増加を緩めてあげればいいんです。
デモ画面にちょうどいいのは、「x座標が64㎝(4マス)変化した時にyが128㎝(8マス)変化する」ようにすればいいわけです。
y=ax^2のaを変える
xが64㎝増加した時、y座標は「64×64=4096㎝」変化します。
これを8マス(128㎝)で割ると、「4096÷128≒32」つまり、「y=1/32x^2」とすればちょうどいいグラフが書けます。
この式の作り方は、また計算ブロックを使います。


このブロックをプログラム画面の余白においてください。
そして、右側に「32」、符号を「 /(÷)」にしてください。
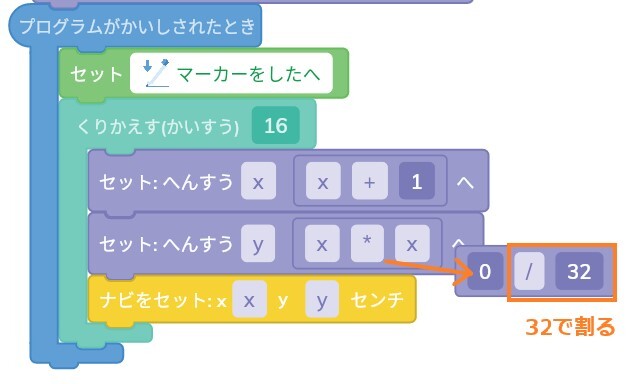

そして、作った式の左側に「x*x」をドラッグして入力します。
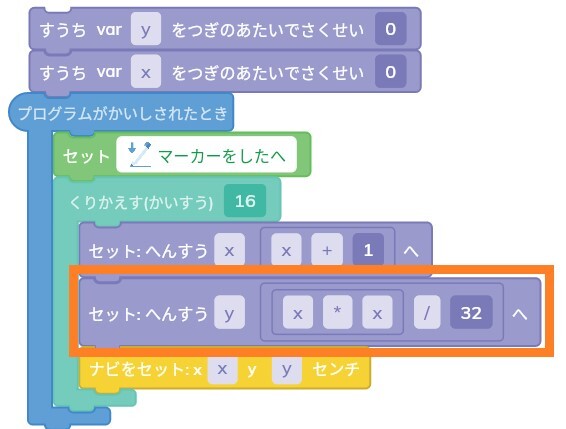

こんな感じにできましたか?
さっそく動かしてみましょう。
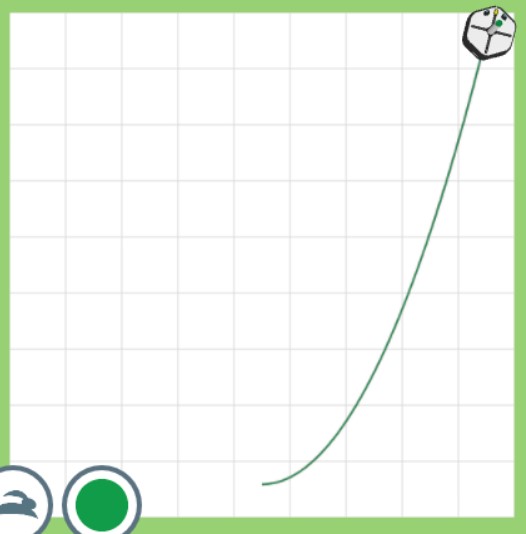




これでちょうどいい二次関数のグラフが書けました!
まとめ
なんとRootで数学の勉強ができるようになりました。
ただのおもちゃから勉強道具に昇格です。
この昇格を喜んでいるのは大人だけかもしれませんけどね・・・